
TRUTH
FUNCTIONAL
CONNECTIVES
1.
Introduction.....................................................................................................28
2.
Statement Connectives....................................................................................28
3.
Truth-Functional Statement Connectives........................................................31
4.
Conjunction.....................................................................................................33
5.
Disjunction ......................................................................................................35
6.
A Statement Connective that is not Truth-Functional.....................................37
7.
Negation ..........................................................................................................38
8.
The Conditional...............................................................................................39
9.
The Non-Truth-Functional Version of If-Then...............................................40
10.
The Truth-Functional Version of If-Then .......................................................41
11.
The Biconditional............................................................................................43
12.
Complex Formulas..........................................................................................44
13.
Truth Tables for Complex Formulas...............................................................46
14.
Exercises for Chapter 2 ...................................................................................54
15.
Answers to Exercises for Chapter 2................................................................57

28
Hardegree, Symbolic Logic
1. INTRODUCTION
As noted earlier, an argument is valid or invalid purely in virtue of its form.
The form of an argument is a function of the arrangement of the terms in the argu-
ment, where the logical terms play a primary role. However, as noted earlier, what
counts as a logical term, as opposed to a descriptive term, is not absolute. Rather, it
depends upon the level of logical analysis we are pursuing.
In the previous chapter we briefly examined one level of logical analysis, the
level of syllogistic logic. In syllogistic logic, the logical terms include ‘all’, ‘some’,
‘no’, ‘are’, and ‘not’, and the descriptive terms are all expressions that denote
classes.
In the next few chapters, we examine a different branch of logic, which repre-
sents a different level of logical analysis; specifically, we examine sentential logic
(also called propositional logic and statement logic). In sentential logic, the logical
terms are truth-functional statement connectives, and nothing else.
2. STATEMENT CONNECTIVES
We begin by defining statement connective, or what we will simply call a
connective.
A (statement) connective is an expression with one or
more blanks (places) such that, whenever the blanks
are filled by statements the resulting expression is also
a statement.
In other words, a (statement) connective takes one or more smaller statements and
forms a larger statement. The following is a simple example of a connective.
___________ and ____________
To say that this expression is a connective is to say that if we fill each blank with a
statement then we obtain another statement. The following are examples of state-
ments obtained in this manner.
(e1) snow is white and grass is green
(e2) all cats are felines and some felines are not cats
(e3) it is raining and it is sleeting
Notice that the blanks are filled with statements and the resulting expressions are
also statements.
The following are further examples of connectives, which are followed by
particular instances.
(c1) it is not true that __________________
(c2) the president believes that ___________
(c3) it is necessarily true that ____________

Chapter 2: Truth-Functional Connectives
29
(c4) __________ or __________
(c5) if __________ then __________
(c6) __________ only if __________
(c7) __________ unless __________
(c8) __________ if __________; otherwise __________
(c9) __________ unless __________ in which case __________
(i1) it is not true that all felines are cats
(i2) the president believes that snow is white
(i3) it is necessarily true that 2+2=4
(i4) it is raining
or it is sleeting
(i5) if it is raining
then it is cloudy
(i6) I will pass
only if I study
(i7) I will play tennis
unless it rains
(i8) I will play tennis
if it is warm; otherwise I will play racquetball
(i9) I will play tennis
unless it rains in which case I will play squash
Notice that the above examples are divided into three groups, according to how
many blanks (places) are involved. This grouping corresponds to the following se-
ries of definitions.
A one-place connective is a connective
with one blank.
A two-place connective is a connective
with two blanks.
A three-place connective is a connective
with three blanks.
etc.
At this point, it is useful to introduce a further pair of definitions.
A compound statement is a statement that is con-
structed from one or more smaller statements by the
application of a statement connective.
A simple statement is a statement that is not con-
structed out of smaller statements by the application of
a statement connective.
We have already seen many examples of compound statements. The
following are examples of simple statements.

30
Hardegree, Symbolic Logic
(s1) snow is white
(s2) grass is green
(s3) I am hungry
(s4) it is raining
(s5) all cats are felines
(s6) some cats are pets
Note that, from the viewpoint of sentential logic, all statements in syllogistic logic
are simple statements, which is to say that they are regarded by sentential logic as
having no internal structure.
In all the examples we have considered so far, the constituent statements are
all simple statements. A connective can also be applied to compound statements, as
illustrated in the following example.
it is not true that all swans are white,
and
the president believes that all swans are white
In this example, the two-place connective ‘...and...’ connects the following two
statements,
it is not true that all swans are white
the president believes that all swans are white
which are themselves compound statements. Thus, in this example, there are three
connectives involved:
it is not true that...
...and...
the president believes that...
The above statement can in turn be used to form an even larger compound
statement. For example, we combine it with the following (simple) statement,
using the two-place connective ‘if...then...’.
the president is fallible
We accordingly obtain the following compound statement.
IF it is not true that all swans are white,
AND the president believes that all swans are white,
THEN the president is fallible
There is no theoretical limit on the complexity of compound statements con-
structed using statement connectives; in principle, we can form compound state-
ments that are as long as we please (say a billion miles long!). However, there are
practical limits to the complexity of compound statements, due to the limitation of
space and time, and the limitation of human minds to comprehend excessively long
and complex statements. For example, I doubt very seriously whether any human

Chapter 2: Truth-Functional Connectives
31
can understand a statement that is a billion miles long (or even one mile long!)
However, this is a practical limit, not a theoretical limit.
By way of concluding this section, we introduce terminology that is often
used in sentential logic.
Simple statements are often referred to as
atomic statements, or simply atoms.
Compound statements are often referred to as
molecular statements, or simply molecules.
The analogy, obviously, is with chemistry. Whereas chemical atoms
(hydrogen, oxygen, etc.) are the smallest chemical units, sentential atoms are the
smallest sentential units. The analogy continues. Although the word ‘atom’ liter-
ally means “that which is indivisible” or “that which has no parts”, we know that
the chemical atoms do have parts (neutrons, protons, etc.); however, these parts are
not chemical in nature. Similarly, atomic sentences have parts, but these parts are
not sentential in nature. These further (sub-atomic) parts are the topic of later
chapters, on predicate logic.
3. TRUTH-FUNCTIONAL STATEMENT CONNECTIVES
In the previous section, we examined the general class of (statement) connec-
tives. At the level we wish to pursue, sentential logic is not concerned with all con-
nectives, but only special ones – namely, the truth-functional connectives.
Recall that a statement is a sentence that, when uttered, is either true or false.
In logic it is customary to refer to truth and falsity as truth values, which are respec-
tively abbreviated T and F. Furthermore, if a statement is true, then we say its truth
value is T, and if a statement is false, then we say that its truth value is F. This is
summarized as follows.
The truth value of a true statement is T.
The truth value of a false statement is F.
The truth value of a statement (say, ‘it is raining’) is analogous to the weight
of a person. Just as we can say that the weight of John is 150 pounds, we can say
that the truth value of ‘it is raining’ is T. Also, John's weight can vary from day to
day; one day it might be 150 pounds; another day it might be 152 pounds.
Similarly, for some statements at least, such as ‘it is raining’, the truth value can
vary from occasion to occasion. On one occasion, the truth value of ‘it is raining’
might be T; on another occasion, it might be F. The difference between weight and
truth-value is quantitative: whereas weight can take infinitely many values (the
positive real numbers), truth value can only take two values, T and F.

32
Hardegree, Symbolic Logic
The analogy continues. Just as we can apply functions to numbers (addition,
subtraction, exponentiation, etc.), we can apply functions to truth values. Whereas
the former are numerical functions, the latter are truth-functions.
In the case of a numerical function, like addition, the input are numbers, and
so is the output. For example, if we input the numbers 2 and 3, then the output is 5.
If we want to learn the addition function, we have to learn what the output number
is for any two input numbers. Usually we learn a tiny fragment of this in
elementary school when we learn the addition tables. The addition tables tabulate
the output of the addition function for a few select inputs, and we learn it primarily
by rote.
Truth-functions do not take numbers as input, nor do they produce numbers as
output. Rather, truth-functions take truth values as input, and they produce truth
values as output. Since there are only two truth values (compared with infinitely
many numbers), learning a truth-function is considerably simpler than learning a
numerical function.
Just as there are two ways to learn, and to remember, the addition tables, there
are two ways to learn truth-function tables. On the one hand, you can simply
memorize it (two plus two is four, two plus three is five, etc.) On the other hand,
you can master the underlying concept (what are you doing when you add two
numbers together?) The best way is probably a combination of these two tech-
niques.
We will discuss several examples of truth functions in the following sections.
For the moment, let's look at the definition of a truth-functional connective.
A statement connective is truth-functional if and only if
the truth value of any compound statement obtained by
applying that connective is a function of (is completely
determined by) the individual truth values of the con-
stituent statements that form the compound.
This definition will be easier to comprehend after a few examples have been dis-
cussed. The basic idea is this: suppose we have a statement connective, call it +,
and suppose we have any two statements, call them S
1
and S
2
. Then we can form a
compound, which is denoted S
1
+S
2
. Now, to say that the connective + is truth-
functional is to say this: if we know the truth values of S
1
and S
2
individually, then
we automatically know, or at least we can compute, the truth value of S
1
+S
2
. On
the other hand, to say that the connective + is not truth-functional is to say this:
merely knowing the truth values of S
1
and S
2
does not automatically tell us the truth
value of S
1
+S
2
. An example of a connective that is not truth-functional is discussed
later.
4. CONJUNCTION
The first truth-functional connective we discuss is conjunction, which cor-
responds to the English expression ‘and’.

Chapter 2: Truth-Functional Connectives
33
[Note: In traditional grammar, the word ‘conjunction’ is used to refer to any two-
place statement connective. However, in logic, the word ‘conjunction’ refers ex-
clusively to one connective – ‘and’.]
Conjunction is a two-place connective. In other words, if we have two state-
ments (simple or compound), we can form a compound statement by combining
them with ‘and’. Thus, for example, we can combine the following two statements
it is raining
it is sleeting
to form the compound statement
it is raining and it is sleeting.
In order to aid our analysis of logical form in sentential logic, we employ
various symbolic devices. First, we abbreviate simple statements by upper case
Roman letters. The letter we choose will usually be suggestive of the statement that
is abbreviated; for example, we might use ‘R’ to abbreviate ‘it is raining’, and ‘S’
to abbreviate ‘it is sleeting’.
Second, we use special symbols to abbreviate (truth-functional) connectives.
For example, we abbreviate conjunction (‘and’) by the ampersand sign (‘&’). Put-
ting these abbreviations together, we abbreviate the above compound as follows.
R & S
Finally, we use parentheses to punctuate compound statements, in a manner
similar to arithmetic. We discuss this later.
A word about terminology, R&S is called a conjunction. More specifically,
R&S is called the conjunction of R and S, which individually are called conjuncts.
By analogy, in arithmetic, x+y is called the sum of x and y, and x and y are indi-
vidually called summands.
Conjunction is a truth-functional connective. This means that if we know the
truth value of each conjunct, we can simply compute the truth value of the conjunc-
tion. Consider the simple statements R and S. Individually, these can be true or
false, so in combination, there are four cases, given in the following table.
R
S
case 1
T
T
case 2
T
F
case 3
F
T
case 4
F
F
In the first case, both statements are true; in the fourth case, both statements are
false; in the second and third cases, one is true, the other is false.
Now consider the conjunction formed out of these two statements: R&S.
What is the truth value of R&S in each of the above cases? Well, it seems plausible
that the conjunction R&S is true if both the conjuncts are true individually, and
R&S is false if either conjunct is false. This is summarized in the following table.

34
Hardegree, Symbolic Logic
R
S
R&S
case 1
T
T
T
case 2
T
F
F
case 3
F
T
F
case 4
F
F
F
The information contained in this table readily generalizes. We do not have
to regard ‘R’ and ‘S’ as standing for specific statements. They can stand for any
statements whatsoever, and this table still holds. No matter what R and S are spe-
cifically, if they are both true (case 1), then the conjunction R&S is also true, but if
one or both are false (cases 2-4), then the conjunction R&S is false.
We can summarize this information in a number of ways. For example, each
of the following statements summarizes the table in more or less ordinary English.
Here, A and B stand for arbitrary statements.
A conjunction A&B is true
if and only if
both conjuncts are true.
A conjunction A&B is true if both conjuncts are true;
otherwise, it is false.
We can also display the truth function for conjunction in a number of ways.
The following three tables present the truth function for conjunction; they are fol-
lowed by three corresponding tables for multiplication.
A
B
A&B
A
&
B
&
T
F
T
T
T
T
T
T
T
T
F
T
F
F
T
F
F
F
F
F
F
T
F
F
F
T
F
F
F
F
F
F
a
b
a×b a
×
b
×
1
0
1
1
1 1
1
1
1
1
0
1
0
0 1
0
0
0
0
0
0
1
0 0
0
1
0
0
0 0
0
0
Note: The middle table is obtained from the first table simply by superimposing
the three columns of the first table. Thus, in the middle table, the truth values of A
are all under the A, the truth values of B are under the B, and the truth values of
A&B are the &. Notice, also, that the final (output) column is also shaded, to help
distinguish it from the input columns. This method saves much space, which is
important later.
We can also express the content of these tables in a series of statements, just
like we did in elementary school. The conjunction truth function may be conveyed

Chapter 2: Truth-Functional Connectives
35
by the following series of statements. Compare them with the corresponding state-
ments concerning multiplication.
(1) T & T = T 1 × 1 = 1
(2) T & F = F 1 × 0 = 0
(3) F & T = F 0 × 1 = 0
(4) F & F = F 0 × 0 = 0
For example, the first statement may be read “T ampersand T is T” (analogously,
“one times one is one”). These phrases may simply be memorized, but it is better
to understand what they are about – namely, conjunctions.
5. DISJUNCTION
The second truth-functional connective we consider is called disjunction,
which corresponds roughly to the English ‘or’. Like conjunction, disjunction is a
two-place connective: given any two statements S
1
and S
2
, we can form the com-
pound statement ‘S
1
or S
2
’. For example, beginning with the following simple
statements,
(s1) it is raining R
(s2) it is sleeting S
we can form the following compound statement.
(c) it is raining or it is sleeting R ∨ S
The symbol for disjunction is ‘∨’ (wedge). Just as R&S is called the conjunction of
R and S, R∨S is called the disjunction of R and S. Similarly, just as the con-
stituents of a conjunction are called conjuncts, the constituents of a disjunction are
called disjuncts.
In English, the word ‘or’ has at least two different meanings, or senses, which
are respectively called the exclusive sense and the inclusive sense. The exclusive
sense is typified by the following sentences.
(e1) would you like a baked potato, OR French fries
(e2) would you like squash, OR beans
In answering these questions, you cannot choose both disjuncts; choosing one dis-
junct excludes choosing the other disjunct.
On the other hand, the inclusive sense of disjunction is typified by the follow-
ing sentences.
(i1) would you like coffee or dessert
(i2) would you like cream or sugar with your coffee
In answering these questions, you can choose both disjuncts; choosing one disjunct
does not exclude choosing the other disjunct as well.

36
Hardegree, Symbolic Logic
Latin has two different disjunctive words, ‘vel’ (inclusive) and ‘aut’
(exclusive). By contrast, English simply has one word ‘or’, which does double
duty. This problem has led the legal profession to invent the expression ‘and/or’
to use when inclusive disjunction is intended. By using ‘and/or’ they are able to
avoid ambiguity in legal contracts.
In logic, the inclusive sense of ‘or’ (the sense of ‘vel’ or ‘and/or’) is taken as
basic; it is symbolized by wedge ‘∨’ (suggestive of ‘v’, the initial letter of ‘vel’).
The truth table for ∨ is given as follows.
A
B
A∨B
A
∨
B
∨
T
F
T
T
T
T
T
T
T
T
T
T
F
T
T
T
F
F
T
F
F
T
T
F
T
T
F
F
F
F
F
F
The information conveyed in these tables can be conveyed in either of the fol-
lowing statements.
A disjunction A∨B is false
if and only if
both disjuncts are false.
A disjunction A∨B is false if both disjuncts are false;
otherwise, it is true.
The following is an immediate consequence, which is worth remembering.
If A is true, then so is A∨B,
regardless of the truth value of B.
If B is true, then so is A∨B,
regardless of the truth value of A.
6. A STATEMENT CONNECTIVE THAT IS NOT TRUTH-
FUNCTIONAL
Conjunction (&) and disjunction (∨) are both truth-functional connectives. In
the present section, we discuss a connective that is not truth-functional – namely,
the connective ‘because’.
Like conjunction (‘and’) and disjunction (‘or’), ‘because’ is a two-place con-
nective; given any two statements S
1
and S
2
, we can form the compound statement
‘S
1
because S
2
’. For example, given the following simple statements

Chapter 2: Truth-Functional Connectives
37
(s1) I am sad S
(s2) it is raining R
we can form the following compound statements.
(c1) I am sad because it is raining S because R
(c2) it is raining because I am sad R because S
The simple statements (s1) and (s2) can be individually true or false, so there
are four possible combinations of truth values. The question is, for each combina-
tion of truth values, what is the truth value of each resulting compound.
First of all, it seems fairly clear that if either of the simple statements is false,
then the compound is false. On the other hand, if both statements are true, then it is
not clear what the truth value of the compound is. This is summarized in the
following partial truth table.
S
R
S because R
R because S
T
T
?
?
T
F
F
F
F
T
F
F
F
F
F
F
In the above table, the question mark (?) indicates that the truth value is unclear.
Suppose both S (‘I am sad’) and R (‘it is raining’) are true. What can we say
about the truth value of ‘S because R’ and ‘R because S’? Well, at least in the case
of
it is raining because I am sad,
we can safely assume that it is false (unless the speaker in question is God, in
which case all bets are off).
On the other hand, in the case of
I am sad because it is raining,
we cannot say whether it is true, or whether it is false. Merely knowing that the
speaker is sad and that it is raining, we do not know whether the rain is responsible
for the sadness. It might be, it might not. Merely knowing the individual truth val-
ues of S (‘I am sad’) and R (‘it is raining’), we do not automatically know the truth
value of the compound ‘I am sad because it is raining’; additional information (of a
complicated sort) is needed to decide whether the compound is true or false. In
other words, ‘because’ is not a truth-functional connective.
Another way to see that ‘because’ is not truth-functional is to suppose to the
contrary that it is truth-functional. If it is truth-functional, then we can replace the
question mark in the above table. We have only two choices. If we replace ‘?’ by
‘T’, then the truth table for ‘R because S’ is identical to the truth table for R&S.
This would mean that for any statements A and B, ‘A because B’ says no more
than ‘A and B’. This is absurd, for that would mean that both of the following
statements are true.

38
Hardegree, Symbolic Logic
grass is green because 2+2=4
2+2=4 because grass is green
Our other choice is to replace ‘?’ by ‘F’. This means that the output column
consists entirely of F's, which means that ‘A because B’ is always false. This is
also absurd, or at least implausible. For surely some statements of the form ‘A
because B’ are true. The following might be considered an example.
grass is green because grass contains chlorophyll
7. NEGATION
So far, we have examined three two-place connectives. In the present section,
we examine a one-place connective, negation, which corresponds to the word ‘not’.
If we wish to deny a statement, for example,
it is raining,
the easiest way is to insert the word ‘not’ in a strategic location, thus yielding
it is not raining.
We can also deny the original statement by prefixing the whole sentence by the
modifier
it is not true that
to obtain
it is not true that it is raining
The advantage of the first strategy is that it produces a colloquial sentence. The
advantage of the second strategy is that it is simple to apply; one simply prefixes
the statement in question by the modifier, and one obtains the denial. Furthermore,
the second strategy employs a statement connective. In particular, the expression
it is not true that ______________
meets our criterion to be a one-place connective; its single blank can be filled by
any statement, and the result is also a statement.
This one-place connective is called negation, and is symbolized by ‘~’
(tilde), which is a stylized form of ‘n’, short for negation. The following are variant
negation expressions.
it is false that __________________
it is not the case that ____________
Next, we note that the negation connective (~) is truth-functional. In other
words, if we know the truth value of a statement S, then we automatically know the
truth value of the negation ~S; the truth value of ~S is simply the opposite of the
truth value of S.

Chapter 2: Truth-Functional Connectives
39
This is plausible. For ~S denies what S asserts; so if S is in fact false, then its
denial (negation) is true, and if S is in fact true, then its denial is false. This is
summarized in the following truth tables.
A
~A
~
A
T
F
F
T
F
T
T
F
In the second table, the truth values of A are placed below the A, and the resulting
truth values for ~A are placed below the tilde sign (~). The right table is simply a
compact version of the left table. Both tables can be summarized in the following
statement.
~A has the opposite truth value of A.
8. THE CONDITIONAL
In the present section, we introduce one of the two remaining truth-functional
connectives that are customarily studied in sentential logic – the conditional con-
nective, which corresponds to the expression
if ___________, then ___________.
The conditional connective is a two-place connective, which is to say that we can
replace the two blanks in the above expression by any two statements, then the
resulting expression is also a statement.
For example, we can take the following simple statements.
(1) I am relaxed
(2) I am happy
and we can form the following conditional statements, using if-then.
(c1) if I am relaxed, then I am happy
(c2) if I am happy, then I am relaxed
The symbol used to abbreviate if-then is the arrow (→), so the above com-
pounds can be symbolized as follows.
(s1) R → H
(s2) H → R
Every conditional statement divides into two constituents, which do not play
equivalent roles (in contrast to conjunction and disjunction). The constituents of a
conditional A→C are respectively called the antecedent and the consequent. The
word ‘antecedent’ means “that which leads”, and the word ‘consequent’ means
“that which follows”. In a conditional, the first constituent is called the antecedent,
and the second constituent is called the consequent. When a conditional is stated in

40
Hardegree, Symbolic Logic
standard form in English, it is easy to identify the antecedent and the consequent,
according to the following rule.
‘if’ introduces the antecedent
‘then’ introduces the consequent
The fact that the antecedent and consequent do not play equivalent roles is re-
lated to the fact that A→C is not generally equivalent to C→A. Consider the
following two conditionals.
if my car runs out of gas, then my car stops R→S
if my car stops, then my car runs out of gas S→R
9. THE NON-TRUTH-FUNCTIONAL VERSION OF IF-THEN
In English, if-then is used in a variety of ways, many of which are not truth-
functional. Consider the following conditional statements.
if I lived in L.A., then I would live in California
if I lived in N.Y.C., then I would live in California
The constituents of these two conditionals are given as follows; note that they are
individually stated in the indicative mood, as required by English grammar.
L: I live in L.A. (Los Angeles)
N: I live in N.Y.C. (New York City)
C: I live in California
Now, for the author at least, all three simple statements are false. But what
about the two conditionals? Well, it seems that the first one is true, since L.A. is
entirely contained inside California (presently!). On the other hand, it seems that
the second one is false, since N.Y.C. does not overlap California.
Thus, in the first case, two false constituents yield a true conditional, but in
the second case, two false constituents yield a false conditional. It follows that the
conditional connective employed in the above conditionals is not truth-functional.
The conditional connective employed above is customarily called the
subjunctive conditional connective, since the constituent statements are usually
stated in the subjunctive mood.
Since subjunctive conditionals are not truth-functional, they are not examined
in sentential logic, at least at the introductory level. Rather, what is examined are
the truth functional conditional connectives.

Chapter 2: Truth-Functional Connectives
41
10. THE TRUTH-FUNCTIONAL VERSION OF IF-THEN
Insofar as we want to have a truth-functional conditional connective, we must
construct its truth table. Of course, since not every use of ‘if-then’ in English is in-
tended to be truth-functional, no truth functional connective is going to be com-
pletely plausible. Actually, the problem is to come up with a truth functional ver-
sion of if-then that is even marginally plausible. Fortunately, there is such a con-
nective.
By way of motivating the truth table for the truth-functional version of ‘if-
then’, we consider conditional promises and conditional requests. Consider the
following promise (made to the intro logic student by the intro logic instructor).
if you get a hundred on every exam, then I will give you an A
which may be symbolized
H→A
Now suppose that the semester ends; under what circumstances has the instructor
kept his/her promise. The relevant circumstances may be characterized as follows.
H
A
case 1:
T
T
case 2:
T
F
case 3:
F
T
case 4:
F
F
The cases divide into two groups. In the first two cases, you get a hundred on
every exam; the condition in question is activated; if the condition is activated, the
question whether the promise is kept simply reduces to whether you do or don't get
an A. In case 1, you get your A; the instructor has kept the promise. In case 2, you
don't get your A, even though you got a hundred on every exam; the instructor has
not kept the promise.
The remaining two cases are different. In these cases, you don't get a hundred
on every exam, so the condition in question isn't activated. We have a choice now
about evaluating the promise. We can say that no promise was made, so no obliga-
tion was incurred; or, we can say that a promise was made, and it was kept by de-
fault.
We follow the latter course, which produces the following truth table.
H
A
H→A
case 1:
T
T
T
case 2:
T
F
F
case 3:
F
T
T
case 4:
F
F
T
Note carefully that in making the above promise, the instructor has not com-
mitted him(her)self about your grade when you don't get a hundred on every exam.
It is a very simple promise, by itself, and may be combined with other promises.

42
Hardegree, Symbolic Logic
For example, the instructor has not promised not to give you an A if you do not get
a hundred on every exam. Presumably, there are other ways to get an A; for
example, a 99% average should also earn an A.
On the basis of these considerations, we propose the following truth table for
the arrow connective, which represents the truth-functional version of ‘if-then’.
A
C
A
→
C
A
→
C
T
T
T
T
T
T
T
F
F
T
F
F
F
T
T
F
T
T
F
F
T
F
T
F
The information conveyed in the above tables may be summarized by either
of the following statements.
A conditional A
→
C is false
if and only if
the antecedent A is true
and the consequent C is false.
A conditional A
→
C is false
if the antecedent A is true
and the consequent C is false;
otherwise, it is true.
11. THE BICONDITIONAL
We have now examined four truth-functional connectives, three of which are
two-place connectives (conjunction, disjunction, conditional), and one of which is a
one-place connective (negation). There is one remaining connective that is
generally studied in sentential logic, the biconditional, which corresponds to the
English
______________if and only if _______________
Like the conditional, the biconditional is a two-place connective; if we fill the
two blanks with statements, the resulting expression is also a statement. For ex-
ample, we can begin with the statements
I am happy
I am relaxed
and form the compound statement
I am happy if and only if I am relaxed

Chapter 2: Truth-Functional Connectives
43
The symbol for the biconditional connective is ‘↔’, which is called double arrow.
The above compound can accordingly be symbolized thus.
H ↔ R
H↔R is called the biconditional of H and R, which are individually called
constituents. The truth table for ↔ is quite simple. One can understand a bicon-
ditional A↔B as saying that the two constituents are equal in truth value; accord-
ingly, A↔B is true if A and B have the same truth value, and is false if they
don't have the same truth value. This is summarized in the following tables.
A
B
A
↔
B
A
↔
B
T
T
T
T
T
T
T
F
F
T
F
F
F
T
F
F
F
T
F
F
T
F
T
F
The information conveyed in the above tables may be summarized by any of
the following statements.
A biconditional A
↔
B is true
if and only if
the constituents A, B have the same truth value.
A biconditional A
↔
B is false
if and only if
the constituents A, B have opposite truth values.
A biconditional A
↔
B is true
if its constituents have the same truth value; otherwise,
it is false.
A biconditional A
↔
B is false
if its constituents have opposite truth values; otherwise,
it is true.
12. COMPLEX FORMULAS
As noted in Section 2, a statement connective forms larger (compound) state-
ments out of smaller statements. Now, these smaller statements may themselves be
compound statements; that is, they may be constructed out of smaller statements by
the application of one or more statement connectives. We have already seen exam-
ples of this in Section 2.
Associated with each statement (simple or compound) is a symbolic abbrevia-
tion, or translation. Each acceptable symbolic abbreviation is what is customarily

44
Hardegree, Symbolic Logic
called a formula. Basically, a formula is simply a string of symbols that is gram-
matically acceptable. Any ungrammatical string of symbols is not a formula.
For example, the following strings of symbols are not
formulas in sentential
logic; they are ungrammatical.
(n1) &∨P(Q
(n2) P&∨Q
(n3) P(∨Q(
(n4) )(P&Q
By contrast, the following strings count as formulas in sentential logic.
(f1) (P & Q)
(f2) (~(P & Q) ∨ R)
(f3) ~(P & Q)
(f4) (~(P & Q) ∨ (P & R))
(f5) ~((P & Q) ∨ (P & R))
In order to distinguish grammatical from ungrammatical strings, we provide
the following formal definition of formula in sentential logic. In this definition, the
script letters stand for strings of symbols. The definition tells us which strings of
symbols are formulas of sentential logic, and which strings are not.
(1) any upper case Roman letter is a formula;
(2) if A is a formula, then so is ~A;
(3) if A and B are formulas, then so is (A & B);
(4) if A and B are formulas, then so is (A ∨ B);
(5) if A and B are formulas, then so is (A → B);
(6) if A and B are formulas, then so is (A ↔ B);
(7) nothing else is a formula.
Let us do some examples of this definition. By clause 1, both P and Q are
formulas, so by clause 2, the following are both formulas.
~P ~Q
So by clause 3, the following are all formulas.
(P & Q) (P & ~Q) (~P & Q) (~P & ~Q)
Similarly, by clause 4, the following expressions are all formulas.
(P ∨ Q) (P ∨ ~Q) (~P ∨ Q) (~P ∨ ~Q)
We can now apply clause 2 again, thus obtaining the following formulas.
~(P & Q) ~(P & ~Q) ~(~P & Q) ~(~P & ~Q)
~(P ∨ Q) ~(P ∨ ~Q) ~(~P ∨ Q) ~(~P ∨ ~Q)
We can now apply clause 3 to any pair of these formulas, thus obtaining the follow-
ing among others.

Chapter 2: Truth-Functional Connectives
45
((P ∨ Q) & (P ∨ ~Q)) ((P ∨ Q) & ~(P ∨ ~Q))
The process described here can go on indefinitely. There is no limit to how long a
formula can be, although most formulas are too long for humans to write.
In addition to formulas, in the strict sense, given in the above definition, there
are also formulas in a less strict sense. We call these strings unofficial formulas.
Basically, an unofficial formula is a string of symbols that is obtained from an offi-
cial formula by dropping the outermost parentheses. This applies only to official
formulas that have outermost parenthesis; negations do not have outer parentheses.
The following is the official definition of an unofficial formula.
An unofficial formula is any string of symbols that is
obtained from an official formula by removing its out-
ermost parentheses (if such exist).
We have already seen numerous examples of unofficial formulas in this chap-
ter. For example, we symbolized the sentence
it is raining and it is sleeting
by the expression
R & S
Officially, the latter is not a formula; however, it is an unofficial formula.
The following represent the rough guidelines for dealing with unofficial for-
mulas in sentential logic.
When a formula stands by itself, one is permitted to
drop its outermost parentheses (if such exist), thus
obtaining an unofficial formula. However, an unofficial
formula cannot be used to form a compound formula.
In order to form a compound, one must restore the
outermost parentheses, thereby converting the unoffi-
cial formula into an official formula.
Thus, the expression ‘R & S’, which is an unofficial formula, can be used to sym-
bolize ‘it is raining and it is sleeting’. On the other hand, if we wish to symbolize
the denial of this statement, which is ‘it is not both raining and sleeting’, then we
must first restore the outermost parentheses, and then prefix the resulting expres-
sion by ‘~’. This is summarized as follows.
it is raining and it is sleeting: R & S
it is not both raining and sleeting: ~(R & S)

46
Hardegree, Symbolic Logic
13. TRUTH TABLES FOR COMPLEX FORMULAS
There are infinitely many formulas in sentential logic. Nevertheless, no matter
how complex a given formula A is, we can compute its truth value, provided we
know the truth values of its constituent atomic formulas. This is because all the
connectives used in constructing A are truth-functional. In order to ascertain the
truth value of A, we simply compute it starting with the truth values of the atoms,
using the truth function tables.
In this respect, at least, sentential logic is exactly like arithmetic. In arith-
metic, if we know the numerical values assigned to the variables x, y, z, we can
routinely calculate the numerical value of any compound arithmetical expression
involving these variables. For example, if we know the numerical values of x, y, z,
then we can compute the numerical value of ((x+y)×z)+((x+y)×(x+z)). This
computation is particularly simple if we have a hand calculator (provided that we
know how to enter the numbers in the correct order; some calculators even solve
this problem for us).
The only significant difference between sentential logic and arithmetic is that,
whereas arithmetic concerns numerical values (1,2,3...) and numerical functions
(+,×, etc.), sentential logic concerns truth values (T, F) and truth functions (&, ∨,
etc.). Otherwise, the computational process is completely analogous. In particular,
one builds up a complex computation on the basis of simple computations, and
each simple computation is based on a table (in the case of arithmetic, the tables are
stored in calculators, which perform the simple computations).
Let us begin with a simple example of computing the truth value of a complex
formula on the basis of the truth values of its atomic constituents. The example we
consider is the negation of the conjunction of two simple formulas P and Q, which
is the formula ~(P&Q). Now suppose that we substitute T for both P and Q; then
we obtain the following expression: ~(T&T). But we know that T&T = T, so
~(T&T) = ~T, but we also know that ~T = F, so ~(T&T) = F; this ends our
computation. We can also substitute T for P and F for Q, in which case we have
~(T&F). We know that T&F is F, so ~(T&F) is ~F, but ~F is T, so ~(T&F) is
T. There are two other cases: substituting F for P and T for Q, and substituting F
for both P and Q. They are computed just like the first two cases. We simply build
up the larger computation on the basis of smaller computations.
These computations may be summarized in the following statements.
case 1: ~(T&T) = ~T = F
case 2: ~(T&F) = ~F = T
case 3: ~(F&T) = ~F = T
case 4: ~(F&F) = ~F = T
Another way to convey this information is in the following table.

Chapter 2: Truth-Functional Connectives
47
Table 1
P
Q
P&Q
~(P&Q)
case 1
T
T
T
F
case 2
T
F
F
T
case 3
F
T
F
T
case 4
F
F
F
T
This table shows the computations step by step. The first two columns are the ini-
tial input values for P and Q; the third column is the computation of the truth value
of the conjunction (P&Q); the fourth column is the computation of the truth value
of the negation ~(P&Q), which uses the third column as input.
Let us consider another simple example of computing the truth value of a
complex formula. The formula we consider is a disjunction of (P&Q) and ~P, that
is, it is the formula (P&Q)∨~P. As in the previous case, there are just two letters,
so there are four combinations of truth values that can be substituted. The
computations are compiled as follows, followed by the corresponding table.
case 1:
(T&T)
∨
~T
=
T
∨
F
=
T
case 2:
(T&F)
∨
~T
=
F
∨
F
=
F
case 3:
(F&T)
∨
~F
=
F
∨
T
=
T
case 4:
(F&F)
∨
~F
=
F
∨
T
=
T
By way of explanation, in case 1, the value of T&T is placed below the &, and the
value of ~T is placed below the ~. These values in turn are combined by the ∨.
Table 2
P
Q
P&Q
~P
(P&Q)∨~P
case 1
T
T
T
F
T
case 2
T
F
F
F
F
case 3
F
T
F
T
T
case 4
F
F
F
T
T
Let's now consider the formula that is obtained by conjoining the first formula
(Table 1) with the second case formula (Table 2); the resulting formula is:
~(P&Q)&((P&Q)∨~P). Notice that the parentheses have been restored on the
second formula before it was conjoined with the first formula. This formula has
just two atomic formulas - P and Q - so there are just four cases to consider. The
best way to compute the truth value of this large formula is simply to take the out-

48
Hardegree, Symbolic Logic
put columns of Tables 1 and 2 and combine them according to the conjunction truth
table.
Table 3
~(P&Q)
(P&Q)∨~P
~(P&Q)&((P&Q)∨~P)
case 1
F
T
F
case 2
T
F
F
case 3
T
T
T
case 4
T
T
T
In case 1, for example, the truth value of ~(P&Q) is F, and the truth value of
(P&Q) ∨ ~P is T, so the value of their conjunction is F&T, which is F. If we were
to construct the table for the complex formula from scratch, we would basically
combine Tables 1 and 2. Table 3 represents the last three columns of such a table.
It might be helpful to see the computation of the truth value for
~(P&Q)&((P&Q)∨~P) done in complete detail for the first case. To begin with,
we write down the formula, and we then substitute in the truth values for the first
case. This yields the following.
~(P & Q) & ((P & Q) ∨ ~P)
case 1: ~(T & T) & ((T & T) ∨ ~T)
The first computation is to calculate T&T, which is T, so that yields
~T & (T ∨ ~T)
The next step is to calculate ~T, which is F, so this yields.
F & (T ∨ F)
Next, we calculate T ∨ F, which is T, which yields.
F & T
Finally, we calculate F&T, which is F, the final result in the computation.
This particular computation can be diagrammed as follows.
~ ( P & Q ) & ( ( P & Q ) ∨ ~ P )
T T T T T
T T F
F T
F
Case 2 can also be done in a similar manner, shown as follows.

Chapter 2: Truth-Functional Connectives
49
~ ( P & Q ) & ( ( P & Q ) ∨ ~ P )
T F T F T
F F F
T F
F
In the above diagrams, the broken lines indicate, in each simple computation,
which truth function (connective) is employed, and the solid lines indicate the input
values.
In principle, in each complex computation involving truth functions, one can
construct a diagram like those above for each case. Unfortunately, however, this
takes up a lot of space and time, so it is helpful to have a more compact method of
presenting such computations. The method that I propose simply involves super-
imposing all the lines above into a single line, so that each case can be presented on
a single line. This can be illustrated with reference to the formulas we have already
discussed.
In the case of the first formula, presented in Table 1, we can present its truth
table as follows.
Table 3
~
(
P
&
Q
)
case 1
F
T
T
T
case 2
T
T
F
F
case 3
T
F
F
T
case 4
T
F
F
F
In this table, the truth values pertaining to each connective are placed beneath that
connective. Thus, for example, in case 1, the first column is the truth value of
~(P&Q), and the third column is the truth value of (P&Q).
We can do the same with Table 2, which yields the following table.
Table 4
(
P
&
Q
)
∨
~
P
case 1
T
T
T
T
F
T
case 2
T
F
F
F
F
T
case 3
F
F
T
T
T
F
case 4
F
F
F
T
T
F
In this table, the second column is the truth value of (P&Q), the fourth column is
the truth value of the whole formula (P&Q)∨~P, and the fifth column is the truth
value of ~P.

50
Hardegree, Symbolic Logic
Finally, we can do the compact truth table for the conjunction of the formulas
given in Tables 3 and 4.
Table 5
~
(
P
&
Q
)
&
(
(
P
&
Q
)
∨
~
P
)
case 1:
F
T
T
T
F
T
T
T
T
F
T
case 2:
T
T
F
F
F
T
F
F
F
F
T
case 3:
T
F
F
T
T
F
F
T
T
T
F
case 4:
T
F
F
F
T
F
F
F
T
T
F
4
3
5
1
3
2
The numbers at the bottom of the table indicate the order in which the columns are
filled in. In the case of ties, this means that the order is irrelevant to the con-
struction of the table.
In constructing compact truth tables, or in computing complex formulas, the
following rules are useful to remember.
DO CONNECTIVES THAT ARE DEEPER BEFORE
DOING CONNECTIVES THAT ARE LESS DEEP.
Here, the depth of a connective is determined by how many pairs of parenthe-
ses it is inside; a connective that is inside two pairs of parentheses is deeper than
one that is inside of just one pair.
AT ANY PARTICULAR DEPTH,
ALWAYS DO NEGATIONS FIRST.
These rules are applied in the above table, as indicated by the numbers at the bot-
tom.
Before concluding this section, let us do an example of a formula that
contains three atomic formulas P, Q, R. In this case, there are 8 combinations of
truth values that can be assigned to the letters. These combinations are given in the
following guide table.
Guide Table for any Formula Involving 3 Atomic Formulas
P Q
R
case 1
T T T
case 2
T T F
case 3
T F T
case 4
T F F
case 5
F T T
case 6
F T F
case 7
F F T
case 8
F F F

Chapter 2: Truth-Functional Connectives
51
There are numerous ways of writing down all the combinations of truth values; this
is just one particular one. The basic rule in constructing this guide table is that the
rightmost column (R) is alternated T and F singly, the middle column (Q) is alter-
nated T and F in doublets, and the leftmost column (P) is alternated T and F in
quadruplets. It is simply a way of remembering all the cases.
Now let's consider a formula involving three letters P, Q, R, and its associated
(compact) truth table.
Table 6
1
2
3
4
5
6
7
8
9
10
P
Q
R
~
[
(
P
&
~
Q
)
∨
(
~
P
∨
R
)
]
T
T
T
F
T
F
F
T
T
F
T
T
T
T
T
F
T
T
F
F
T
F
F
T
F
F
T
F
T
F
T
T
T
F
T
F
T
T
T
T
F
F
F
T
T
T
F
T
F
T
F
F
F
T
T
F
F
F
F
T
T
T
F
T
T
F
T
F
F
F
F
F
T
T
T
F
T
F
F
F
T
F
F
F
T
F
T
T
F
T
T
F
F
F
F
F
F
T
F
T
T
F
T
F
5
1
3
2
1
4
2
1
3
1
The guide table is not required, but is convenient, and is filled in first. The remain-
ing columns, numbered 1-10 at the top, completed in the order indicated at the bot-
tom. In the case of ties, the order doesn't matter.
In filling a truth table, it is best to understand the structure of the formula. In
case of the above formula, it is a negation; in particular it is the negation of the for-
mula (P&~Q)∨(~P∨R). This formula is a disjunction, where the individual dis-
juncts are P&~Q and P∨R respectively. The first disjunct P&~Q is a conjunction
of P and the negation of Q; the second disjunct ~P∨R is a disjunction of ~P and R.
The structure of the formula is crucial, and is intimately related to the order in
which the truth table is filled in. In particular, the order in which the table is filled
in is exactly opposite from the order in which the formula is broken into its con-
stituent parts, as we have just done.
In filling in the above table, the first thing we do is fill in three columns under
the letters, which are the smallest parts; these are labeled 1 at the bottom. Next, we
do the negations of letters, which corresponds to columns 4 and 7, but not column
1. Column 4 is constructed from column 5 on the basis of the tilde truth table, and
column 7 is constructed from column 8 in a like manner. Next column 3 is con-
structed from columns 2 and 4 according to the ampersand truth table, and column
9 is constructed from columns 7 and 10 according to the wedge truth table. These
two resulting columns, 3 and 9, in turn go into constructing column 6 according to
the wedge truth table. Finally, column 6 is used to construct column 1 in
accordance with the negation truth table.
The first two cases are diagrammed in greater detail below.
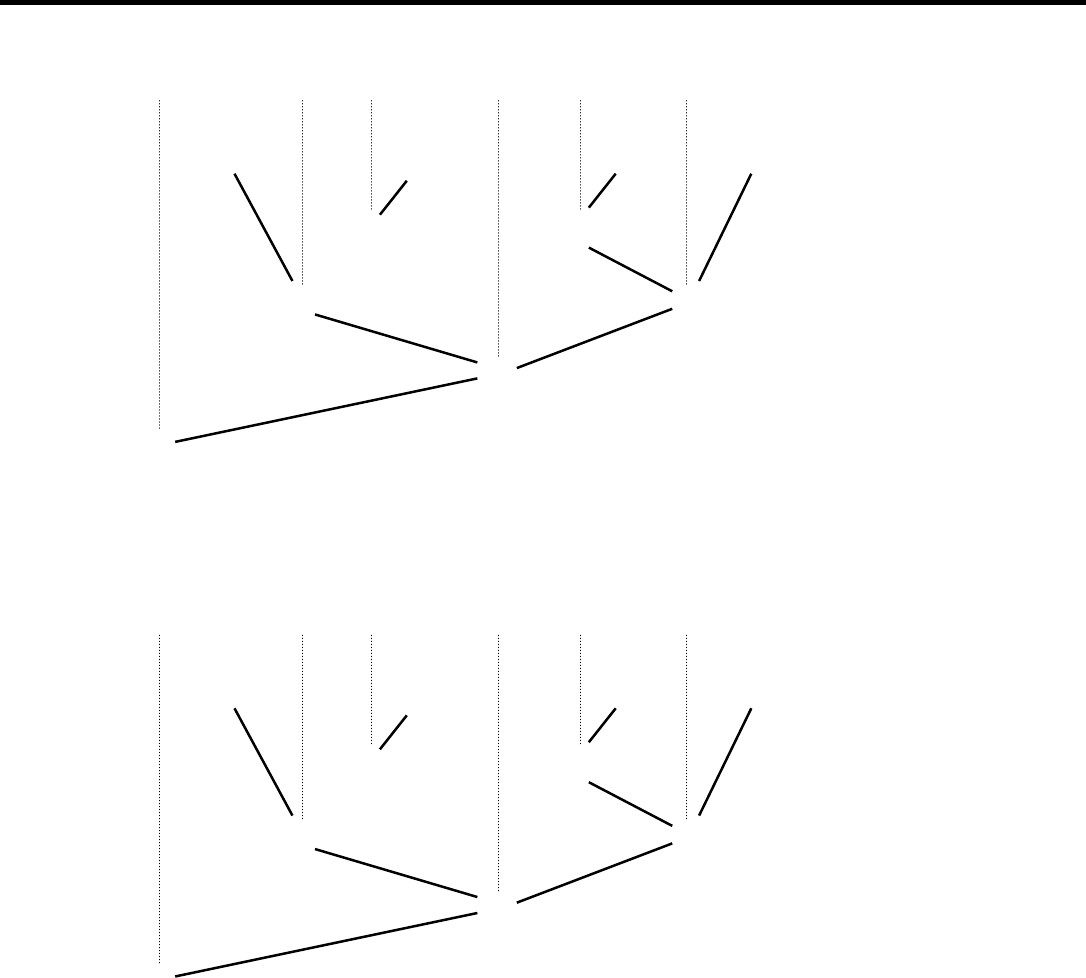
52
Hardegree, Symbolic Logic
~ [ ( P & ~ Q ) ∨ ( ~ P ∨ R ) ]
T T T T
F F
F T
T
F
~ [ ( P & ~ Q ) ∨ ( ~ P ∨ R ) ]
T T T F
F F
F F
F
T
As in our previous example, the broken lines indicate which truth function is ap-
plied, and the solid lines indicate the particular input values, and output values.

Chapter 2: Truth-Functional Connectives
53
14. EXERCISES FOR CHAPTER 2
EXERCISE SET A
Compute the truth values of the following symbolic statements, supposing that the
truth value of A, B, C is T, and the truth value of X, Y, Z is F.
1. ~A ∨ B
2. ~B ∨ X
3. ~Y ∨ C
4. ~Z ∨ X
5. (A & X) ∨ (B & Y)
6. (B & C) ∨ (Y & Z)
7. ~(C & Y) ∨ (A & Z)
8. ~(A & B) ∨ (X & Y)
9. ~(X & Z) ∨ (B & C)
10. ~(X & ~Y) ∨ (B & ~C)
11. (A ∨ X) & (Y ∨ B)
12. (B ∨ C) & (Y ∨ Z)
13. (X ∨ Y) & (X ∨ Z)
14. ~(A ∨ Y) & (B ∨ X)
15. ~(X ∨ Z) & (~X ∨ Z)
16. ~(A ∨ C) ∨ ~(X & ~Y)
17. ~(B ∨ Z) & ~(X ∨ ~Y)
18. ~[(A ∨ ~C) ∨ (C ∨ ~A)]
19. ~[(B & C) & ~(C &B)]
20. ~[(A & B) ∨ ~(B & A)]
21. [A ∨ (B ∨ C)] & ~[(A ∨ B) ∨ C]
22. [X ∨ (Y & Z)] ∨ ~[(X ∨ Y) & (X ∨ Z)]
23. [A & (B ∨ C)] & ~[(A & B) ∨ (A & C)]
24. ~{[(~A & B) & (~X & Z)] & ~[(A & ~B) ∨ ~(~Y & ~Z)]}
25. ~{~[(B & ~C) ∨ (Y & ~Z)] & [(~B ∨ X) ∨ (B ∨ ~Y)]}

54
Hardegree, Symbolic Logic
EXERCISE SET B
Compute the truth values of the following symbolic statements, supposing that the
truth value of A, B, C is T, and the truth value of X, Y, Z is F.
1. A → B
2. A → X
3. B → Y
4. Y → Z
5. (A → B) → Z
6. (X → Y) → Z
7. (A → B) → C
8. (X → Y) → C
9. A → (B → Z)
10. X → (Y → Z)
11. [(A → B) → C] → Z
12. [(A → X) → Y] → Z
13. [A → (X → Y)] → C
14. [A → (B → Y)] → X
15. [(X → Z) → C] → Y
16. [(Y → B) → Y] → Y
17. [(A → Y) → B] → Z
18. [(A & X) → C] → [(X → C) → X]
19. [(A & X) → C] → [(A → X) → C]
20. [(A & X) → Y] → [(X → A) → (A → Y)]
21. [(A & X) ∨ (~A & ~X)] → [(A → X) & (X → A)]
22. {[A → (B → C)] → [(A & B) → C]} → [(Y → B) → (C → Z)]
23. {[(X → Y) → Z] → [Z → (X → Y)]} → [(X → Z) → Y]
24. [(A & X) → Y] → [(A → X) & (A → Y)]
25. [A → (X & Y)] → [(A → X) ∨ (A → Y)]

Chapter 2: Truth-Functional Connectives
55
EXERCISE SET C
Construct the complete truth table for each of the following formulas.
1. (P & Q) ∨ (P & ~Q)
2. ~(P & ~P)
3. ~(P ∨ ~P)
4. ~(P&Q)∨(~P∨~Q)
5. ~( P ∨ Q) ∨ (~P & ~Q)
6. (P & Q) ∨ (~P & ~Q)
7. ~(P ∨ (P & Q))
8. ~(P ∨ (P & Q)) ∨ P
9. (P & (Q ∨ P)) & ~P
10. ((P → Q) → P) → P
11. ~(~(P → Q) → P)
12. (P → Q) ↔ ~P
13. P → (Q → (P & Q))
14. (P ∨ Q) ↔ (~P → Q)
15. ~(P ∨ (P → Q))
16. (P → Q) ↔ (Q → P)
17. (P → Q) ↔ (~Q → ~P)
18. (P ∨ Q) → (P & Q)
19. (P & Q) ∨ (P & R)
20. [P → (Q & R)] → [P → R]
21. [P → (Q ∨ R)] → [P → Q]
22. [(P ∨ Q) → R] → [P → R]
23. [(P & Q) → R] → [P → R]
24. [(P & Q) → R] → [(Q & ~R) → ~P]
25. [P ↔ (Q ↔ R)] ↔ [(P ↔ Q) ↔ R]

56
Hardegree, Symbolic Logic
15. ANSWERS TO EXERCISES FOR CHAPTER 2
EXERCISE SET A
1. T 14. F
2. F 15. T
3. T 16. T
4. T 17. F
5. F 18. F
6. T 19. T
7. T 20. F
8. F 21. F
9. T 22. T
10. T 23. F
11. T 24. T
12. F 25. F
13. F
EXERCISE SET B
1. T 14. T
2. F 15. F
3. F 16. T
4. T 17. F
5. F 18. F
6. F 19. T
7. T 20. F
8. T 21. T
9. F 22. F
10. T 23. F
11. F 24. F
12. F 25. T
13. T

Chapter 2: Truth-Functional Connectives
57
EXERCISE SET C
1.
(
P
&
Q
)
∨
(
P
&
~
Q
)
T
T
T
T
T
F
F
T
T
F
F
T
T
T
T
F
F
F
T
F
F
F
F
T
F
F
F
F
F
F
T
F
2.
~
(
P
&
~
P
)
T
T
F
F
T
T
F
F
T
F
3.
~
(
P
∨
~
P
)
F
T
T
F
T
F
F
T
T
F
4.
~
(
P
&
Q
)
∨
(
~
P
∨
~
Q
)
F
T
T
T
F
F
T
F
F
T
T
T
F
F
T
F
T
T
T
F
T
F
F
T
T
T
F
T
F
T
T
F
F
F
T
T
F
T
T
F
5.
~
(
P
∨
Q
)
∨
(
~
P
&
~
Q
)
F
T
T
T
F
F
T
F
F
T
F
T
T
F
F
F
T
F
T
F
F
F
T
T
F
T
F
F
F
T
T
F
F
F
T
T
F
T
T
F
6.
(
P
&
Q
)
∨
(
~
P
&
~
Q
)
T
T
T
T
F
T
F
F
T
T
F
F
F
F
T
F
T
F
F
F
T
F
T
F
F
F
T
F
F
F
T
T
F
T
T
F
7.
~
(
P
∨
(
P
&
Q
)
)
F
T
T
T
T
T
F
T
T
T
F
F
T
F
F
F
F
T
T
F
F
F
F
F
8.
~
(
P
∨
(
P
&
Q
)
)
∨
P
F
T
T
T
T
T
T
T
F
T
T
T
F
F
T
T
T
F
F
F
F
T
T
F
T
F
F
F
F
F
T
F
9.
(
P
&
(
Q
∨
P
)
)
&
~
P
T
T
T
T
T
F
F
T
T
T
F
T
T
F
F
T
F
F
T
T
F
F
T
F
F
F
F
F
F
F
T
F
10.
(
(
P
→
Q
)
→
P
)
→
P
T
T
T
T
T
T
T
T
F
F
T
T
T
T
F
T
T
F
F
T
F
F
T
F
F
F
T
F
11.
~
(
~
(
P
→
Q
)
→
P
)
F
F
T
T
T
T
T
F
T
T
F
F
T
T
F
F
F
T
T
T
F
F
F
F
T
F
T
F
12.
(
P
→
Q
)
↔
~
P
T
T
T
F
F
T
T
F
F
T
F
T
F
T
T
T
T
F
F
T
F
T
T
F
13.
P
→
(
Q
→
(
P
&
Q
)
)
T
T
T
T
T
T
T
T
T
F
T
T
F
F
F
T
T
F
F
F
T
F
T
F
T
F
F
F

58
Hardegree, Symbolic Logic
14.
(
P
∨
Q
)
↔
(
~
P
→
Q
)
T
T
T
T
F
T
T
T
T
T
F
T
F
T
T
F
F
T
T
T
T
F
T
T
F
F
F
T
T
F
F
F
15.
~
(
P
∨
(
P
→
Q
)
)
F
T
T
T
T
T
F
T
T
T
F
F
F
F
T
F
T
T
F
F
T
F
T
F
16
(
P
→
Q
)
↔
(
Q
→
P
)
T
T
T
T
T
T
T
T
F
F
F
F
T
T
F
T
T
F
T
F
F
F
T
F
T
F
T
F
17.
(
P
→
Q
)
↔
(
~
Q
→
~
P
)
T
T
T
T
F
T
T
F
T
T
F
F
T
T
F
F
F
T
F
T
T
T
F
T
T
T
F
F
T
F
T
T
F
T
T
F
18.
(
P
∨
Q
)
→
(
P
&
Q
)
T
T
T
T
T
T
T
T
T
F
F
T
F
F
F
T
T
F
F
F
T
F
F
F
T
F
F
F
19.
(
P
&
Q
)
∨
(
P
&
R
)
T
T
T
T
T
T
T
T
T
T
T
T
F
F
T
F
F
T
T
T
T
T
F
F
F
T
F
F
F
F
T
F
F
F
T
F
F
T
F
F
F
F
F
F
F
F
F
F
T
F
F
F
F
F
F
F
20.
[
P
→
(
Q
&
R
)
]
→
[
P
→
R
]
T
T
T
T
T
T
T
T
T
T
F
T
F
F
T
T
F
F
T
F
F
F
T
T
T
T
T
T
F
F
F
F
T
T
F
F
F
T
T
T
T
T
F
T
T
F
T
T
F
F
T
F
T
F
F
T
F
F
T
T
F
T
T
F
T
F
F
F
T
F
T
F
21.
[
P
→
(
Q
∨
R
)
]
→
[
P
→
Q
]
T
T
T
T
T
T
T
T
T
T
T
T
T
F
T
T
T
T
T
T
F
T
T
F
T
F
F
T
F
F
F
F
T
T
F
F
F
T
T
T
T
T
F
T
T
F
T
T
T
F
T
F
T
T
F
T
F
T
T
T
F
T
F
F
T
F
F
F
T
F
T
F
22.
[
(
P
∨
Q
)
→
R
]
→
[
P
→
R
]
T
T
T
T
T
T
T
T
T
T
T
T
F
F
T
T
F
F
T
T
F
T
T
T
T
T
T
T
T
F
F
F
T
T
F
F
F
T
T
T
T
T
F
T
T
F
T
T
F
F
T
F
T
F
F
F
F
T
T
T
F
T
T
F
F
F
T
F
T
F
T
F

Chapter 2: Truth-Functional Connectives
59
23.
[
(
P
&
Q
)
→
R
]
→
[
P
→
R
]
T
T
T
T
T
T
T
T
T
T
T
T
F
F
T
T
F
F
T
F
F
T
T
T
T
T
T
T
F
F
T
F
F
T
F
F
F
F
T
T
T
T
F
T
T
F
F
T
T
F
T
F
T
F
F
F
F
T
T
T
F
T
T
F
F
F
T
F
T
F
T
F
24.
[
(
P
&
Q
)
→
R
]
→
[
(
Q
&
~
R
)
→
~
P
]
T
T
T
T
T
T
T
F
F
T
T
F
T
T
T
T
F
F
T
T
T
T
F
F
F
T
T
F
F
T
T
T
F
F
F
T
T
F
T
T
F
F
T
F
T
F
F
T
F
T
F
T
F
F
T
T
T
T
T
F
F
T
T
T
F
F
F
T
T
F
T
T
T
T
F
T
T
F
F
F
F
T
T
T
F
F
F
T
T
T
F
F
F
F
T
F
T
F
F
T
F
T
T
F
25.
[
P
↔
(
Q
↔
R
)
]
↔
[
(
P
↔
Q
)
↔
R
]
T
T
T
T
T
T
T
T
T
T
T
T
F
T
F
F
T
T
T
T
F
F
T
F
F
F
T
T
T
F
F
F
T
T
T
F
T
F
T
T
F
F
T
F
F
F
T
T
T
T
F
F
T
F
T
F
T
T
F
F
T
F
F
T
T
F
F
T
F
F
T
T
F
T
F
T
T
F
F
F
T
F
T
F
T
F
F
F
